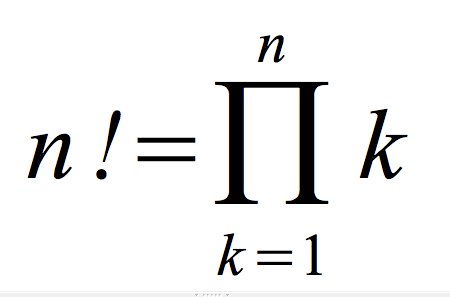¿Alguna vez has escuchado sobre la leyenda del problema 6? Este fue en realidad un problema que hizo tropezar a un ganador de la medalla Fields. Este problema ha sido considerado como uno de los más difíciles en las olimpiadas de matemáticas internacionales del siglo pasado.
Personalmente, me tomó meses resolver este problema e imaginar que a estos concursantes se les daba 6 horas para resolverlo, ¿quién soy yo para creer resolverlo en menos de ese tiempo?
Este problema se hizo particularmente famoso por haberse llevado a cabo el 16 de julio de 1988 en Canberra, Australia; dónde Terrence Tao participó y ganó la medalla de oro en esa olimpiada internacional de matemáticas.

Terence Tao a la edad de 10 años con el prominente matemático Paul Erdos.
Sean {a, b} enteros positivos tal que ab+1 dividan ![]() . Mostrar que:
. Mostrar que:
![]()
Es igual al cuadrado de un número entero positivo.
Para esto tenemos dos posibilidades 1) el resultado es igual a una fracción, por lo tanto no es un número entero y eso anula la respuesta como válida. 2) el resultado es un número entero positivo elevado al cuadrado.
Si encontraste el resultado; ¡Felicidades! Ahora puedes compartir este problema con tus amigos.
Guillermo Cuadra